Dinámica v3.2 es un programa que permite obtener la respuesta sísmica de una obra civil o inmueble, modelada como un oscilador (péndulo invertido), cuando es sometida a una fuerza de aceleración en su base.
Es una aplicación de escritorio (para S.O. Windows) de libre uso enfocada principalmente a los profesores que imparten la materia de Ingeniería símica y a los alumnos que la cursan. Pero también, puede ser de utilidad para cualquier persona con conocimientos de estructuras (ingeniería civil) que necesite una herramienta para aprender conceptos básicos de la dinámica estructural.
Está diseñado principalmente para obtener la respuesta numérica y mostrar animaciones de los osciladores con determinadas propiedades dinámicas sometidos a una fuerza de aceleración. Con este sistema también es posible obtener los espectros de respuesta así como su animación respectiva.
Uno de los objetivos es que el usuario pueda reproducir los resultados de la respuesta numérica que realice por otros medios, la documentación en PDF del sistema contiene el algoritmo de cálculo que utiliza el programa.
El programa es la actualización de la versión anterior (v3.1) que forma parte de la Tesis de grado de maestría del Ing. Octavio Hinojoza bajo la dirección del Dr. Mario Ordaz, en el posgrado de Ingeniería de la UNAM (Ciudad de México) en el año 2009.
Consideraciones
La principal finalidad es ser una herramienta de ayuda para la enseñanza y el aprendizaje de la ingeniería sísmica. El programa surge como una ayuda tanto para el profesor como para los alumnos y es imprescindible que se tome al programa sólo como una herramienta del tema.
El desarrollo de esta aplicación intenta fomentar el interés en los alumnos el tema de dinámica estructural, un ejercicio interesante es mostrar en clase las animaciones del comportamiento de los osciladores y las gráficas de respuesta.
En cuanto a temas técnicos, el programa sólo puede mostrar estructuras modeladas como osciladores de uno hasta 50 grados de libertad con propiedades elástico-lineales. Y el cálculo de la respuesta dinámica se realizará con una aproximación numérica de la integral de Duhamel; conocido también como el método de las ocho constantes.
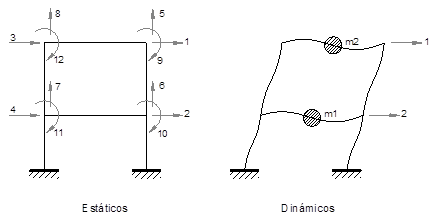
El modelo del oscilador representa a estructuras simples, es decir, que todo su peso o masa se considera concentrada en un solo punto y está sostenida por un resorte que toma el valor de la rigidez lateral de la estructura. El sistema proporciona al usuario una serie de fuerzas de excitación predeterminadas como vibración libre, armónica, pulso y además algunos registros sísmicos almacenados en su base de datos; además, el usuario puede ingresar su archivo de entrada si así lo requiere.
.
Metodología de cálculo
Para determinar la respuesta dinámica se resuelve la ecuación del equilibrio dinámico con una aproximación numérica de la integral de Duhamel, que es un método numérico altamente eficiente para sistemas lineales. Consiste en determinar la respuesta de desplazamiento y velocidad para cada intervalo de tiempo por medio de la ayuda de constantes (4 para desplazamiento y 4 para velocidad) que se calculan una sola vez en el procedimiento.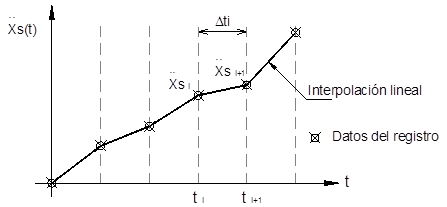 
El método es especialmente eficiente (Chopra A. K. (2001), “Dynamics of structures: theory and applications to earthquake engineering” Second edition, Prentice Hall, EUA) cuando el registro de aceleraciones (excitación en la base) tiene un intervalo de tiempo (Dt) constante entre cada dato del registro, y además, supone una relación lineal entre ellos. Si los intervalos (Dt) son pequeños la interpolación lineal se considera satisfactoria.